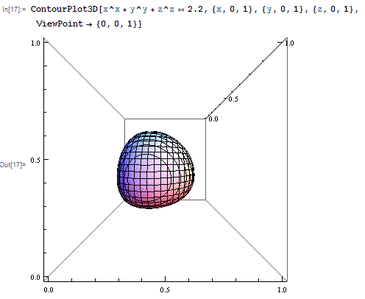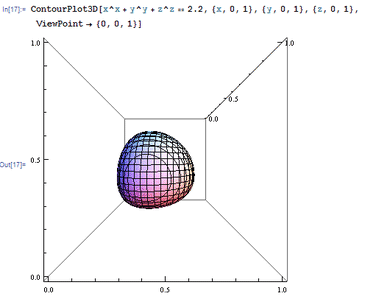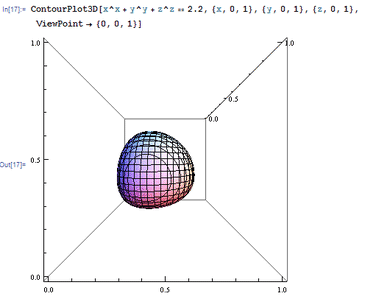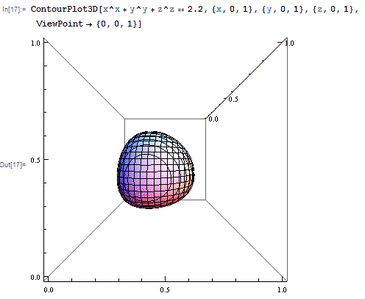
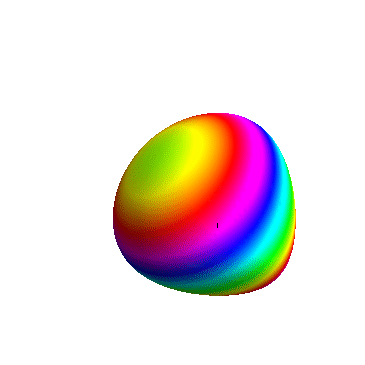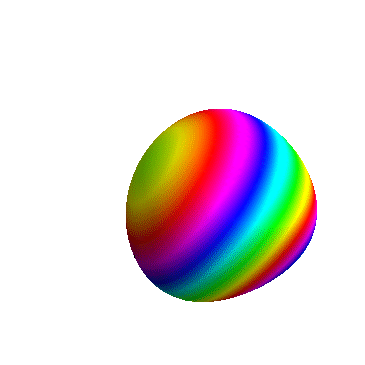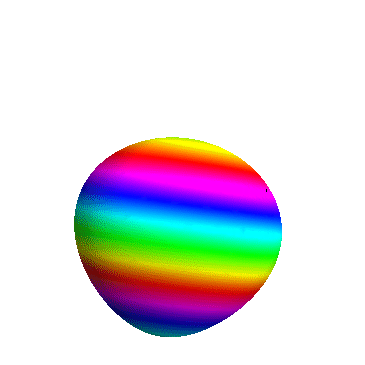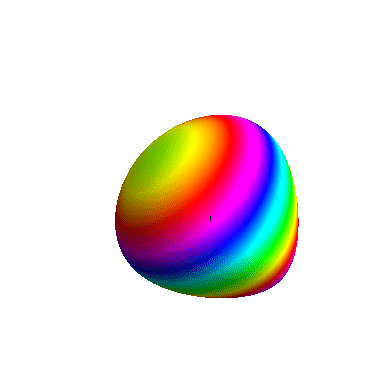1、 ViewPoint,直译为观察点,Graphics3D[3D图形, ViewPoint -> {a,b,c}]表示你观察3D图形的坐标位于{a,b,c}。 举个例子:ContourPlot3D[x^x + y^y + z^z == 2,2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, ViewPoint -> {0, 0, 1}] 此时的观察点位于{0, 0, 1}处。
2、 如果把不同位置观察到的3D图形放到一起,就会呈现3D图形的旋转效果。举例如下:Animate[ContourPlot3D[ x^x + y^y + z^z == 2,2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, ViewPoint -> {Cos[t], Sin[t], 0}, Axes -> False,{t,o, 2 Pi}] 而观察点所经过的路径是:ParametricPlot3D[{Cos[t],Sin[t], 0}, {t, 0, 2 Pi}]。 奇怪的是,3D图形旋转的时候很不稳定,忽远忽近。
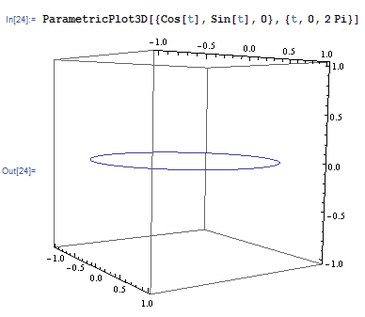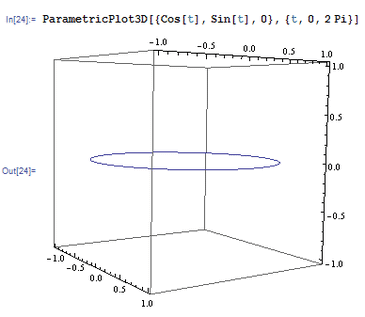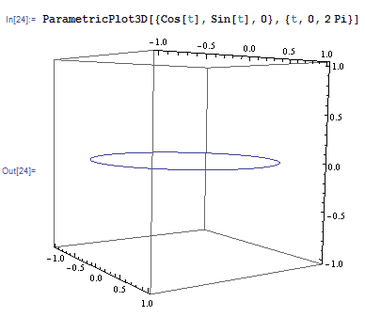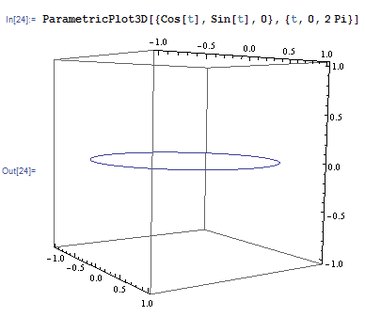

3、 这里引进一个选项——SphericalRegion,直译为球形区域,作用是把被观察的图形限制在一个球形区域内部,可以解决上面那个3D图形“突突乱跳”的现象。注意,SphericalRegion -> True是紧跟在ViewPoint选项后面的!Animate[ContourPlot3D[ x^x + y^y + z^z == 2.2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, ViewPoint -> 5 {Cos[t], Sin[t], o},SphericalRegion -> True, Axes -> False], {t, 0, 2 Pi}] 然后发现,整个图形变大了,以至于我们不能够完整地看到全图,这是因为我们距离图形太近了。

4、 “不识庐山真面目,只缘身在此山中”! 所以,我们可以把观察点的位置拉远一点,这样就可以观察3D图形的整体了:Animate[ContourPlot3D[ x^x + y^y + z^z == 2.2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, ViewPoint -> 3 {Cos[t], Sin[t], 0}, SphericalRegion -> True, Axes -> False,], {t, 0, 2 Pi}] 我们把观察点的距离拉远了3倍,效果如下图。
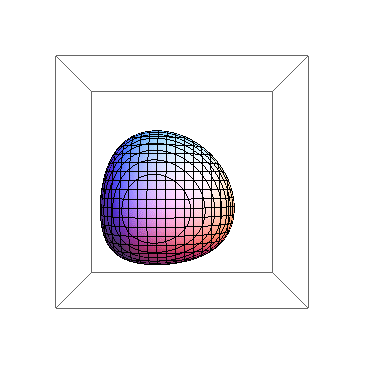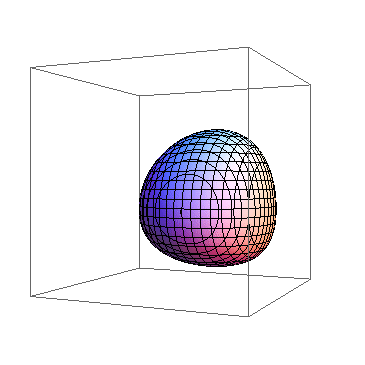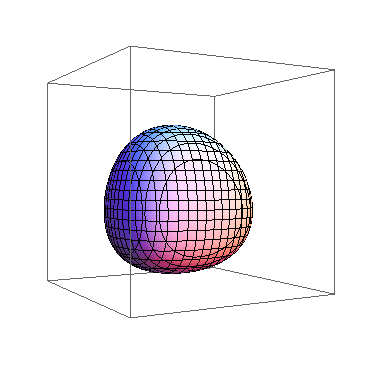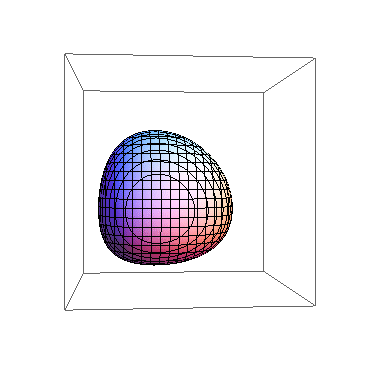
5、 感觉这种旋转之下,我们不能看到图形的各个角度的不同情形。我们希望3D图形全方位旋转,上下、左右、前后都有。 这就要从观察点的路径着眼了,观察路径要足够的复杂。我们用如下的观察路径:ParametricPlot3d[{Cos[t] Sin[t], Cos[t]'2, Sin[t]}, {t, 0, 2 Pi}]

6、 用这个路径来试试:Animate[ContourPlot3D职邗珩垃[ x^x + y^y + z^z == 2.2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, 蕺清寤凯ViewPoint -> {Cos[t] Sin[t], Cos[t]^2, Sin[t]}, SphericalRegion -> True,Axes -> False], {t, 0, 2 Pi}] 再把距离拉远5倍:Animate[Cont0urPlot3D[ x^x + y^y + z^z == 2.2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, ViewPoint -> 5 {Cos[t]Sin[t], Cos[t]^2, Sin[t]}, SphericalRegion -> True, Axes -> False], {t, 0, 2 Pi}]


7、 最后,来一个精彩示例,绘制旋转的3D彩色图形,并且把边框、网坼黉赞楞格线都去掉,适当的拉近观察距离:Animate[ContourPlot3D[ x^x + y^y + z^z == 2.2, {x, 0, 1}, {y, 0, 1}, {z, 0, 1}, ViewPoint -> 2 {Cos[t] Sin[t], Cos[t]^2, Sin[t]}, SphericalRegion -> True, Axes -> False, Boxed -> False, Mesh -> None, ColorFunction -> Function[{x, y, z}, Hue[x + y + z]]],{t, 0, 2 Pi}] 结果如图。