在初中的学习阶段,我们会学到一些有关平面几何和解析几何的知识。通过以往积累的解题经撰颧幌汪验,我们发现有时候我们既可以用平面几何知参萝治璃识来解某道几何题,也可用解析几何的知识来解这道题。当然解析几何知识的应用是建立在平面几何知识的基础上,也就是解析几何和平面几何是有某种内在联系的。下面我通过用两种方法解一道几何题目,来说明初中生如何选用平面几何或解析几何来解几何题。
工具/原料
初中平面几何和解析几何基础知识
用“平面几何知识”来解答
1、选用“平面几何知识”来解答的原则阅读题目完毕后,作出相应的图形,不费什么时间就发现某些图形存在某种联系,比如某两个三角形存在相似关系等;对几何图形具有敏锐的观察力,熟悉平面几何中的有关知识,比如相似三角形等知识。
2、分析原题题目要我们求∠AFD的大小,我们可以想到“把∠AFD放在某个三角形中,利用三角形的内角和等于180°来求解”;若把∠AFD聚刁擞蛔放在△BFG中来解的话,我们发现并不好解,因为根据题意,我们只能得出△BFG是一个直角三角形,∠BGF和∠AFD都是未知的;所以我们可以尝试做辅助线,连接BE,在△BFE中,求解∠AFD,在具体解题过程中,这里会用到“正方形的某些性质”以及“相似三角形的某些结论”等知识。
3、做辅助线连接BE;
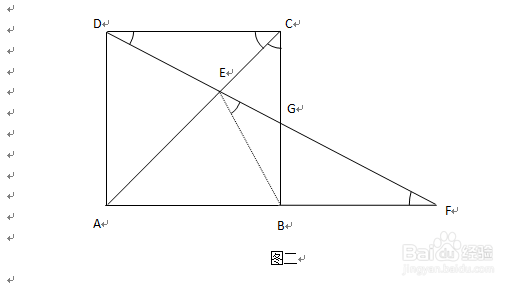
4、具体解答过程已知四边形ABCD是正方形,则CDC幞洼踉残B;AC是正方形ABCD的对角线,则∠ACD∠ACB;又在△DCE和△BCE中,CE是柬缰缣挞公共边;则由三角形相似的判定定理之一,“如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似;简叙为:两边对应成比例且夹角相等”得,△CED≌△CEB;则得DE=BE,∠CDE=∠CBE;已知点F在AB的延长线上,则CD∥AF,则得∠CDE=∠GFB;已知∠CDE=∠CBE,且∠CDE=∠GFB;则得∠CBE=∠GFB;已知DE=BE,且DE=BF,则得BE=BF,即△BEF为等腰三角形;则得∠BEF=∠BFE;综上可得,在△BFE中,∠GBE=∠BFE,∠BEF=∠BFE;又已知CB垂直AF,则得∠GBF=90°,根据“三角形的内角和等于180°”,则得∠BFE+∠BEF+∠EBF=180°即∠BFE+∠BEF+(∠EBG+∠GBF) =180°即∠BFE+∠BFE +(∠BFE +90°) =180°即3∠BFE=90°即∠BFE=30°则∠AFD=30°.
用“解析几何知识”来解答
1、选用“解析几何知识”来解答的原则可以在原图形的基础上快速建立平面直角坐标系;没有发现或者不易发现各个图形之间的联系;细心,具有较强的计算功底。
2、建立直角坐标系因为四边形ABCD是正方形,所以我们以正方形ABCD的某个顶点为原点,可以很方便的建立平面直角坐标系,具体建坐标系的方法如下:我们在图三中建立了以点A为原点O,以正方形的边AB所在的直线为x轴,以正方形的边AD所在的直线为y轴,并对x轴和y轴分别规定了合适的正方向。
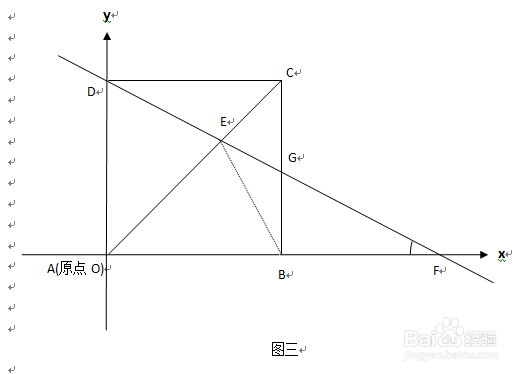
3、列方程以及求解

