1、 介绍用代点计算法等由圆x^2+y^2=1外一点(2,5)引圆的割线交圆于A、B两点,求弦AB的中点M的轨迹方程。
2、 此时圆x^2+y^2=1与点p(2,5)在同一坐标系示意图为。
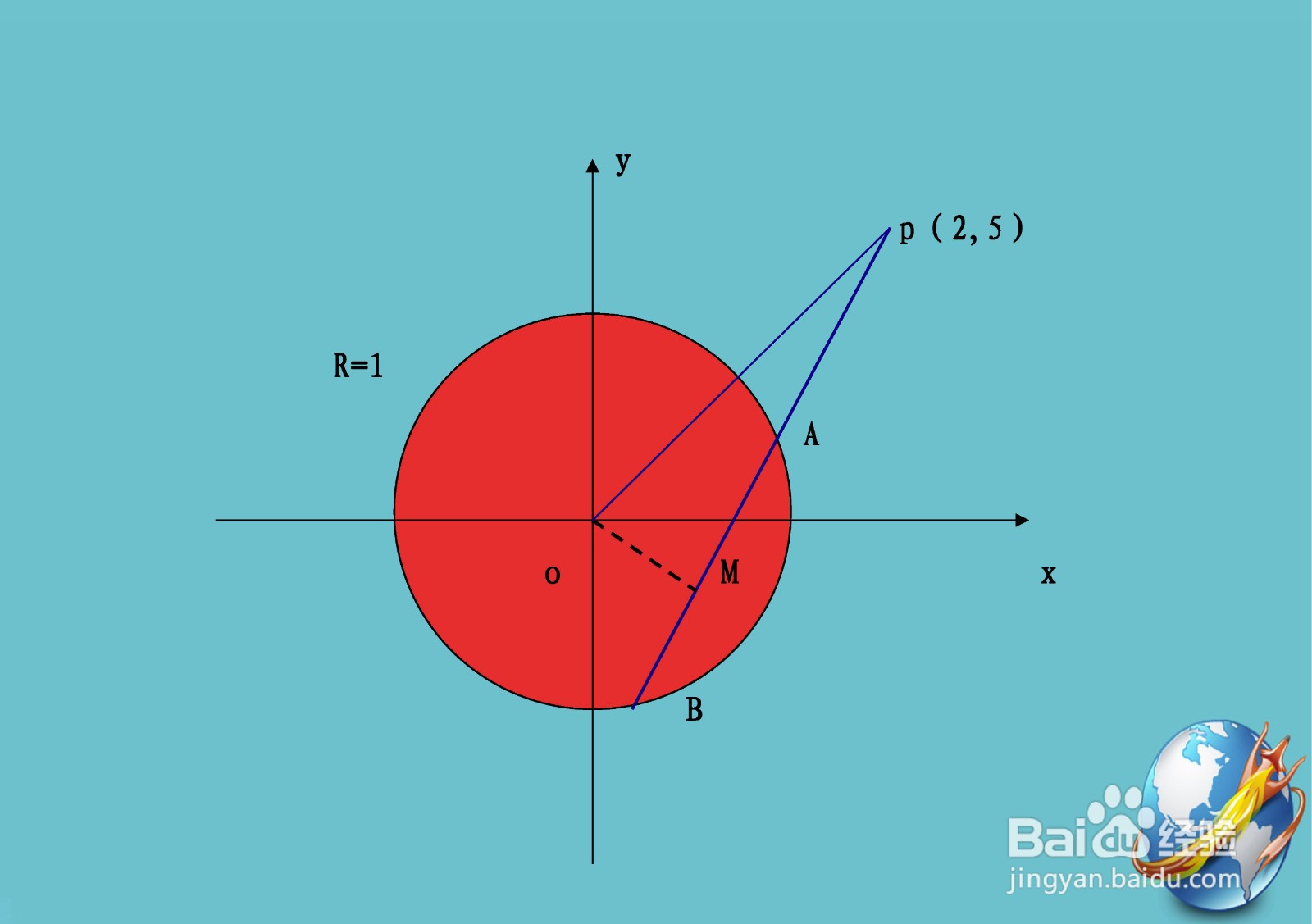
3、 圆是一种几何图形,指的是平面中到一个定点距离为定值的所有点的集合。这个给定的点称为圆的圆心。作为定值的距离称为圆的半径。
当一条线段绕着它的一个端点在平面内旋转一周时,它的另一个端点的轨迹就是一个圆。
圆的直径有无数条;圆的对称轴有无数条。圆的直径是半径的2倍,圆的半径是直径的一半。

1、运用解析几何基本公式转化为代数等式,并根据在圆x^2+y^2=1中有关弦中点的一些性质,圆心和弦中点的连线垂直于弦,从而求出轨迹方程。

2、轨迹性质定义法,根据题设条件,判断并确定轨迹的曲线类型,运用待定系数法求出曲线方程。

3、动点M可看作直线OM与割线PM的交点,而由于它们的垂直关系,从而获得解法。

4、参数求轨迹法,将动点坐标表示成某一中间变量即参数的函数,再设法消去参数。由于动点M(x0,y0)随直线的斜率变化而发生变化,所以动点M的坐标是直线斜率的函数。


5、点在曲线上则点的坐标满足方程。这里由于中点M的坐标(x,y)与两交点A(x1,y1),B(x2,y2)通过中点公式联系起来,又点P、M、A、B构成4点共线,根据它们的斜率相等,可求得轨迹方程。

6、化简计算所得方程,即可得本题所求的轨迹方程。


7、点在曲线上则点的坐标满足方程。这里由于中点M的坐标(x,y)与两交点A(x1,y1),B(x2,y2)通过中点公式联系起来,又点P、M、A、B构成4点共线,根据它们的斜率相等,可求得轨迹方程。


8、 轨迹方程,符合一定条件的动点所形成的图形,或者说,符合一定条件的点的全体所组成的集合,叫做满足该条件的点的轨迹,平面轨迹一般是曲线,空间轨迹一般是曲面。
9、求动点的轨迹方程,主要有定义法、相关点法和参数法等。
定义法:如果能够确定动点的轨迹满足某种已知曲线的定义,则可利用曲线的定义写出方程,这种求轨迹方程的方法叫作定义法.
相关点法:用动点Q的坐标x,y表示相关点P的坐标x0、y0,然后代入点P的坐标(x0,y0)所满足的曲线方程,整理化简便得到动点Q轨迹方程,这种求轨迹方程的方法叫作相关点法.
参数法:当动点坐标x、y之间的直接关系难以找到时,往往先寻找x、y与某一变数t的关系,得再消去参变数t,得到方程,即为动点的轨迹方程,这种求轨迹方程的方法叫作参数法.
