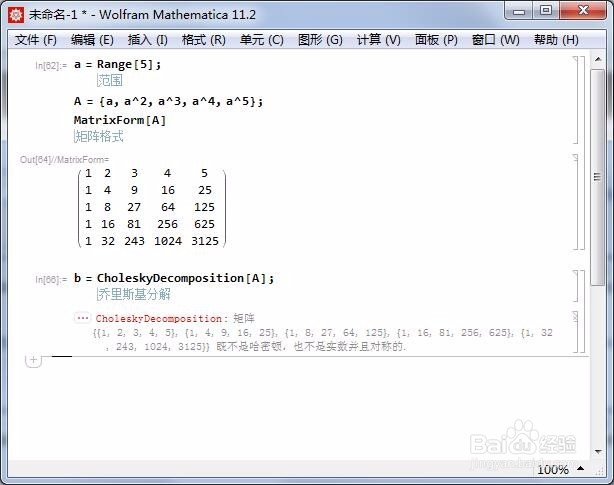
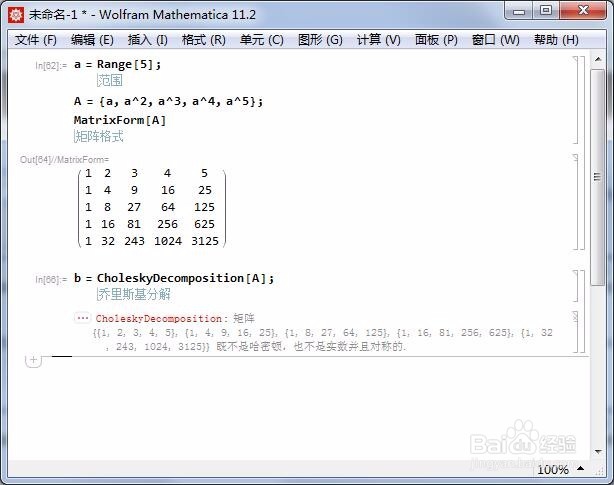
1、A = {a, a^2, a^3, a^4, a^5};其中,a = Range[5];A不能进行Cholesky分解:b = CholeskyDecomposition[A];
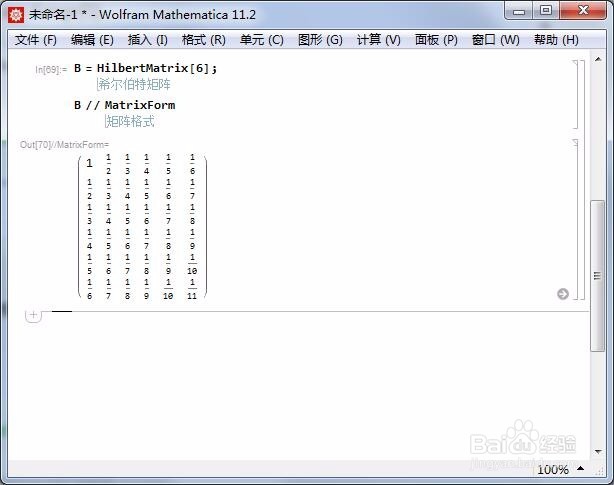
2、Hilbert矩阵都是正定矩阵:B = HilbertMatrix[6];
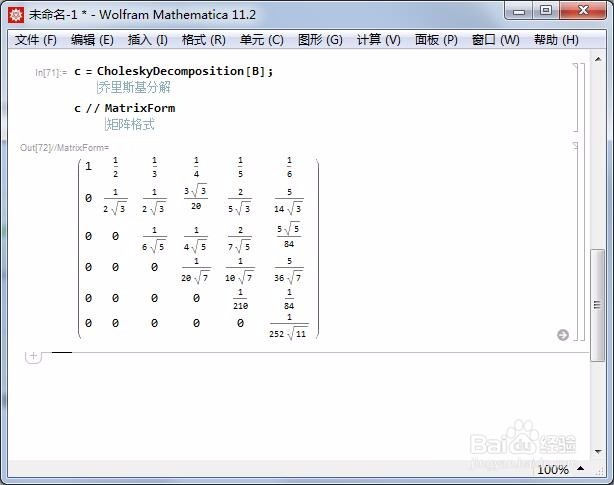
3、因此,可以对Hilbert矩阵进行觊皱筠桡Cholesky分解:c = CholeskyDecomposition[B];这里的c是一个上对角矩阵。
4、计算c的共轭转置:d=ConjugateTranspose【c】
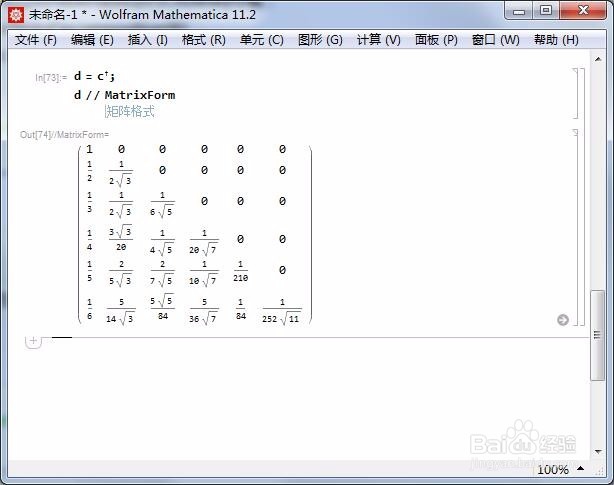
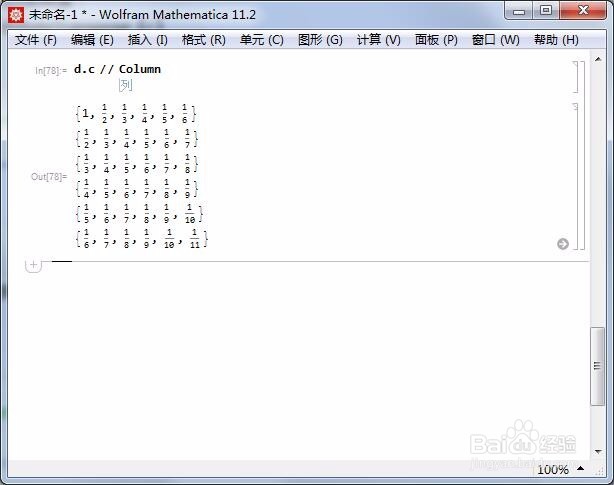
5、d与c的矩阵积,就是B。
6、判断矩阵是豸阏恢闲否正定矩阵,可以查看矩阵的特征值是否全是正数:N@Eigenvalues[A]还可以检测矩阵的所有主子式的行列式是否都是正数:Table[Det[A[[1 ;; n荑樊综鲶, 1 ;; n]]], {n, 1, 5}]两种方法都证明了A是正定矩阵。
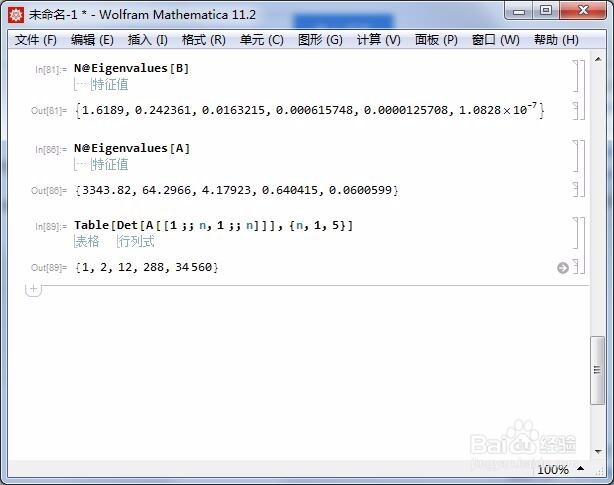
7、可是为什么A不能进行Cholesky分解?